Mathematics Notes VIII

Rational Number

(Ex.1 all questions)

Ex 1.1 Class 8 Maths Question 1.

Using appropriate properties find:

Solution:

Ex 1.1 Class 8 Maths Question 2.
Write the additive inverse of each of the following:
(i) 28
(ii) −59
(iii) −6−5
(iv) 2−9
(v) 19−6
Solution:

Ex 1.1 Class 8 Maths Question 3.
Verify that -(-x) = x for
(i) x = 115
(ii) x = −1317
Solution:

Ex 1.1 Class 8 Maths Question 4.
Find the multiplicative inverse of the following:

Solution:

Ex 1.1 Class 8 Maths Question 5.
Name the property under multiplication used in each of the following:


Solution:
(i) Commutative property of multiplication
(ii) Commutative property of multiplication
(iii) Multiplicative inverse property

Ex 1.1 Class 8 Maths Question 6.
Multiply 613 by the reciprocal of −716.
Solution:

Ex 1.1 Class 8 Maths Question 7.
Tell what property allows you to compute

Solution:
Since a × (b × c) = (a × b) × c shows the associative property of multiplications.

Ex 1.1 Class 8 Maths Question 8.
Is 89 the multiplicative inverse of -118? Why or Why not?
Solution:
Here -118 = −98.
Since multiplicative inverse of 89 is 98 but not −98
89 is not the multiplicative inverse of -118

Ex 1.1 Class 8 Maths Question 9.
If 0.3 the multiplicative inverse of 313? Why or why not?
Solution:

Multiplicative inverse of 0.3 or 310 is 103.
Thus, 0.3 is the multiplicative inverse of 313.

Ex 1.1 Class 8 Maths Question 10.
Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution:
(i) 0 is the rational number which does not have its reciprocal
[∵ 10 is not defined]
(ii) Reciprocal of 1 = 11 = 1
Reciprocal of -1 = 1−1 = -1
Thus, 1 and -1 are the required rational numbers.
(iii) 0 is the rational number which is equal to its negative.

Ex 1.1 Class 8 Maths Question 11.
Fill in the blanks.
(i) Zero has ……….. reciprocal.
(ii) The numbers ……….. and ……….. are their own reciprocals.
(iii) The reciprocal of -5 is ………
(iv) Reciprocal of 1x, where x ≠ 0 is ……….
(v) The product of two rational numbers is always a …………
(vi) The reciprocal of a positive rational number is ……….
Solution:
(i) no
(ii) -1 and 1
(iii) −15
(iv) x
(v) rational number
(vi) positive

• Chapter 2: Linear Equations in One Variable.

• 
  

• Ex 2.1 Class 8 Maths Question 1.
  Solve the equation: x – 2 = 7.
  Solution:
  Given: x – 2 = 7
  ⇒ x – 2 + 2 = 7 + 2 (adding 2 on both sides)
  ⇒ x = 9 (Required solution)

  Ex 2.1 Class 8 Maths Question 2.
  Solve the equation: y + 3 = 10.
  Given: y + 3 = 10
  ⇒ y + 3 – 3 = 10 – 3 (subtracting 3 from each side)
  ⇒ y = 7 (Required solution)

  Ex 2.1 Class 8 Maths Question 3.
  Solve the equation: 6 = z + 2
  Solution:
  We have 6 = z + 2
  ⇒ 6 – 2 = z + 2 – 2 (subtracting 2 from each side)
  ⇒ 4 = z
  Thus, z = 4 is the required solution.

  Ex 2.1 Class 8 Maths Question 4.
  Solve the equations: 37 + x = 177
  Solution: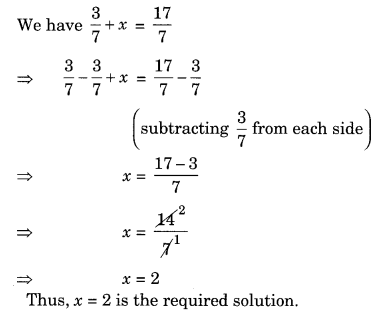
  

  Ex 2.1 Class 8 Maths Question 5.
  Solve the equation 6x = 12.
  Solution:
  We have 6x = 12
  ⇒ 6x ÷ 6 = 12 ÷ 6 (dividing each side by 6)
  ⇒ x = 2
  Thus, x = 2 is the required solution.

  Ex 2.1 Class 8 Maths Question 6.
  Solve the equation t5 = 10.
  Solution:
  Given t5 = 10
  ⇒ t5 × 5 = 10 × 5 (multiplying both sides by 5)
  ⇒ t = 50
  Thus, t = 50 is the required solution.

  Ex 2.1 Class 8 Maths Question 7.
  Solve the equation 2x3 = 18.
  Solution:
  We have 2x3 = 18
  ⇒ 2x3 × 3 = 18 × 3 (multiplying both sides by 3)
  ⇒ 2x = 54
  ⇒ 2x ÷ 2 = 54 ÷ 2 (dividing both sides by 2)
  ⇒ x = 27
  Thus, x = 27 is the required solution.

  Ex 2.1 Class 8 Maths Question 8.
  Solve the equation 1.6 = y1.5
  Solution:
  Given: 1.6 = y1.5
  ⇒ 1.6 × 1.5 = y1.5 × 1.5 (multiplying both sides by 1.5)
  ⇒ 2.40 = y
  Thus, y = 2.40 is the required solution.

  Ex 2.1 Class 8 Maths Question 9.
  Solve the equation 7x – 9 = 16.
  Solution:
  We have 7x – 9 = 16
  ⇒ 7x – 9 + 9 = 16 + 9 (adding 9 to both sides)
  ⇒ 7x = 25
  ⇒ 7x ÷ 7 = 25 ÷ 7 (dividing both sides by 7)
  ⇒ x = 257
  Thus, x = 257 is the required solution.

  Ex 2.1 Class 8 Maths Question 10.
  Solve the equation 14y – 8 = 13.
  Solution:
  We have 14y – 8 = 13
  ⇒ 14y – 8 + 8 = 13 + 8 (adding 8 to both sides)
  ⇒ 14y = 21
  ⇒ 14y ÷ 14 = 21 ÷ 14 (dividing both sides by 14)
  ⇒ y = 2114
  ⇒ y = 32
  Thus, y = 32 is the required solution.

  Ex 2.1 Class 8 Maths Question 11.
  Solve the equation 17 + 6p = 9.
  Solution:
  We have, 17 + 6p = 9
  ⇒ 17 – 17 + 6p = 9 – 17 (subtracting 17 from both sides)
  ⇒ 6p = -8
  ⇒ 6p ÷ 6 = -8 ÷ 6 (dividing both sides by 6)
  ⇒ p = −86
  ⇒ p = −43
  Thus, p = −43 is the required solution.

  Ex 2.1 Class 8 Maths Question 12.
  Solve the equation x3 + 1 = 715
  Solution: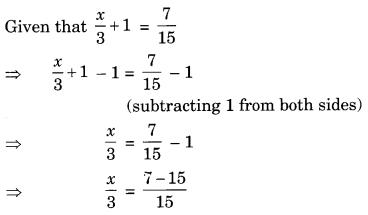
  

  

  

  

  

  

  

  

  

  

  

  

  

  

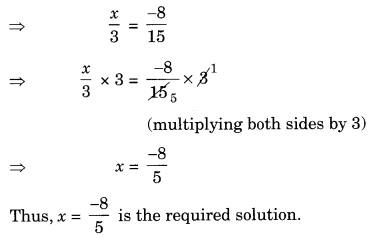
• Ch:3 Understanding Quadrilaterals

• 
  

• Ex 3.1 Class 8 Maths Question 1.
  Given here are some figures.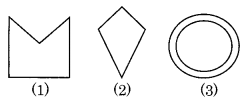
  

  
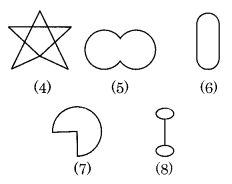
  Classify each of the above figure on the basis of the following:
  (a) Simple curve
  (b) Simple closed curve
  (c) Polygon
  (d) Convex polygon
  (e) Concave polygon
  Solution:
  (a) Simple curve: (1), (2), (5), (6) and (7)
  (b) Simple closed curve: (1), (2), (5), (6) and (7)
  (c) Polygon: (1) and (2)
  (d) Convex polygon: (2)
  (e) Concave polygon: (1)

  Ex 3.1 Class 8 Maths Question 2.
  How many diagonals does each of the following have?
  (a) A convex quadrilateral
  (b) A regular hexagon
  (c) A triangle
  Solution:
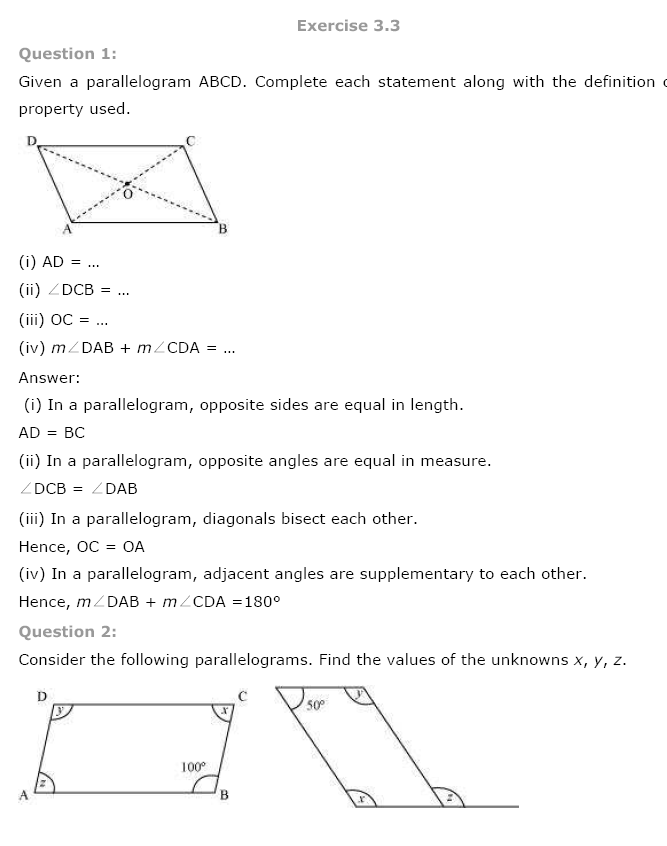
  (a) In Fig. (i) ABCD is a convex quadrilateral which has two diagonals AC and BD.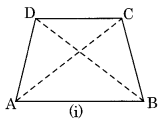
  
  (b) In Fig. (ii) ABCDEF is a regular hexagon which has nine diagonals AE, AD, AC, BF, BE, BD, CF, CE and DF.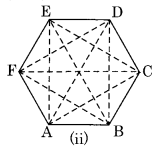
  
  (c) In Fig. (iii) ABC is a triangle which has no diagonal.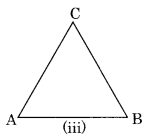
  

  Ex 3.1 Class 8 Maths Question 3.
  What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and verify)
  Solution:
  In the given figure, we have a quadrilateral ABCD. Join AC diagonal which divides the quadrilateral into two triangles ABC and ADC.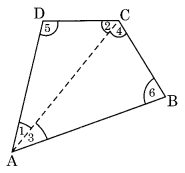
  
  In ∆ABC, ∠3 + ∠4 + ∠6 = 180°…(i) (angle sum property)
  In ∆ADC, ∠1 + ∠2 + ∠5 = 180° …(ii) (angle sum property)
  Adding, (i) and (ii)
  ∠1 + ∠3 + ∠2 + ∠4 + ∠5 + ∠6 = 180° + 180°
  ⇒ ∠A + ∠C + ∠D + ∠B = 360°
  Hence, the sum of all the angles of a convex quadrilateral = 360°.
  Let us draw a non-convex quadrilateral.
  Yes, this property also holds true for a non-convex quadrilateral.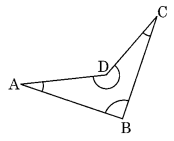
  

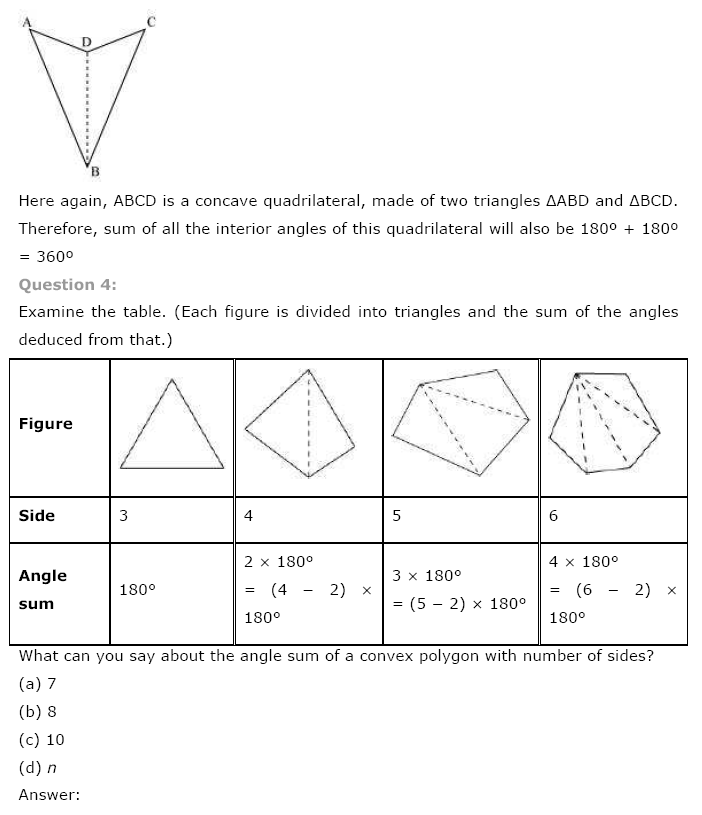
  Ex 3.1 Class 8 Maths Question 4.
  Examine the table. (Each figure is divided into triangles and the sum of the angles reduced from that).
  
  What can you say about the angle sum of a convex polygon with number of sides?
  (a) 7
  (b) 8
  (c) 10
  (d) n
  Solution:
  From the above table, we conclude that the sum of all the angles of a polygon of side ‘n’
  = (n – 2) × 180°
  (a) Number of sides = 7
  Angles sum = (7 – 2) × 180° = 5 × 180° = 900°
  (b) Number of sides = 8
  Angle sum = (8 – 2) × 180° = 6 × 180° = 1080°
  (c) Number of sides = 10 Angle sum = (10 – 2) × 180° = 8 × 180° = 1440°
  (d) Number of sides = n
  Angle sum = (n – 2) × 180°

  Ex 3.1 Class 8 Maths Question 5.
  What is a regular polygon? State the name of a regular polygon of
  (i) 3 sides
  (ii) 4 sides
  (iii) 6 sides
  Solution:
  A polygon with equal sides and equal angles is called a regular polygon.
  (i) Equilateral triangle
  
  (ii) Square
  
  (iii) Regular Hexagon
  

  Ex 3.1 Class 8 Maths Question 6.
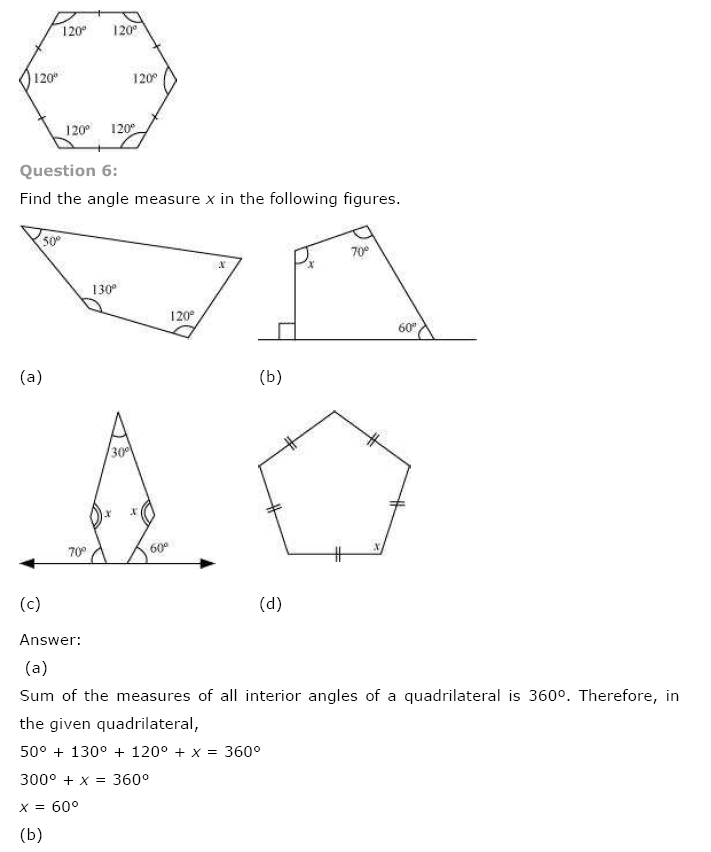
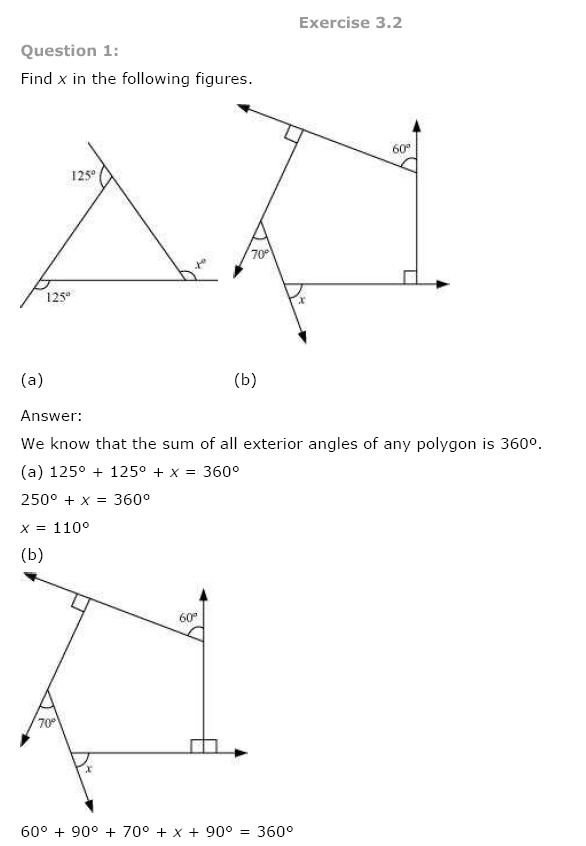
  Find the angle measure x in the following figures: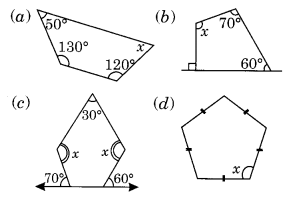
  
  Solution:
  (a) Angle sum of a quadrilateral = 360°
  ⇒ 50° + 130° + 120° + x = 360°
  ⇒ 300° + x = 360°
  ⇒ x = 360° – 300° = 60°
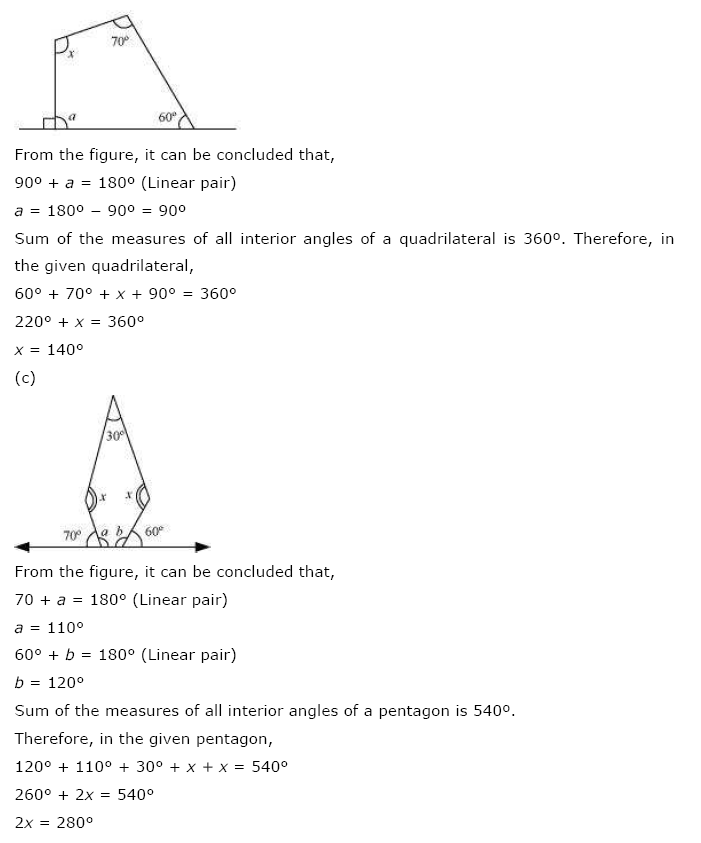
  (b) Angle sum of a quadrilateral = 360°
  ⇒ x + 70° + 60° + 90° = 360° [∵ 180° – 90° = 90°]
  ⇒ x + 220° = 360°
  ⇒ x = 360° – 220° = 140°
  (c) Angle sum of a pentagon = 540°
  ⇒ 30° + x + 110° + 120° + x = 540° [∵ 180° – 70° = 110°; 180° – 60° = 120°]
  ⇒ 2x + 260° = 540°
  ⇒ 2x = 540° – 260°
  ⇒ 2x = 280°
  ⇒ x = 140°
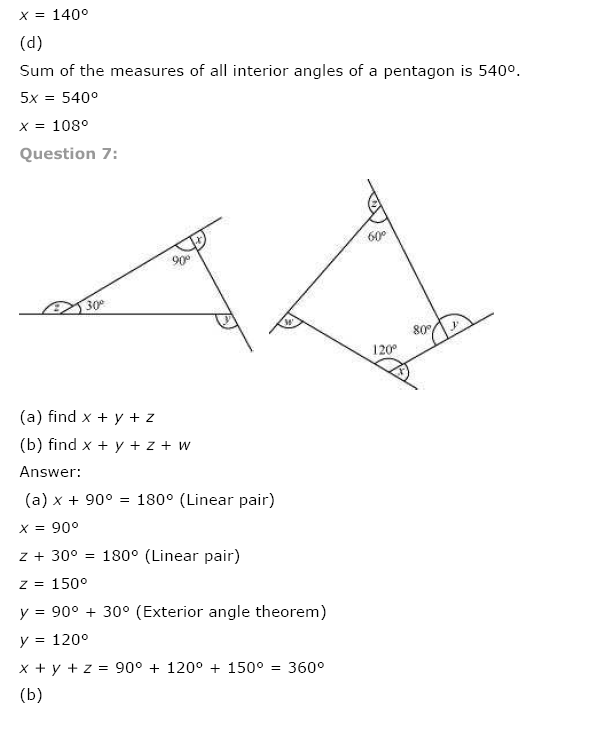
  (d) Angle sum of a regular pentagon = 540°
  ⇒ x + x + x + x + x = 540° [All angles of a regular pentagon are equal]
  ⇒ 5x = 540°
  ⇒ x = 108°

  Ex 3.1 Class 8 Maths Question 7.
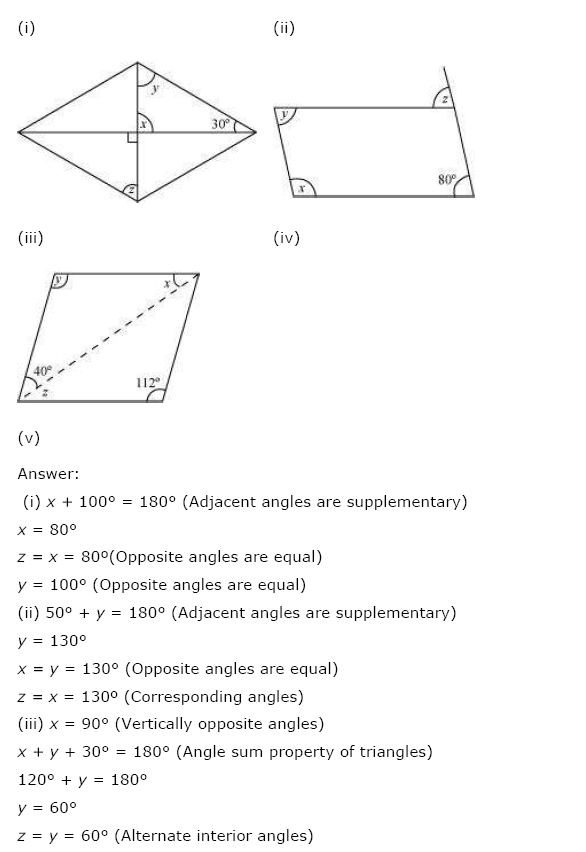
  (a) Find x + y + z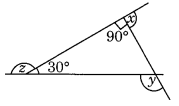
  
  (b) Find x + y + z + w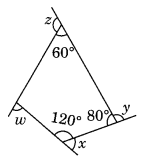
  
  Solution:
  (a) ∠a + 30° + 90° = 180° [Angle sum property]
  ⇒ ∠a + 120° = 180°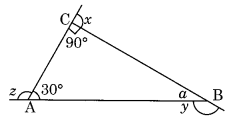
  
  ⇒ ∠a = 180° – 120° = 60°
  Now, y = 180° – a (Linear pair)
  ⇒ y = 180° – 60°
  ⇒ y = 120°
  and, z + 30° = 180° [Linear pair]
  ⇒ z = 180° – 30° = 150°
  also, x + 90° = 180° [Linear pair]
  ⇒ x = 180° – 90° = 90°
  Thus x + y + z = 90° + 120° + 150° = 360°
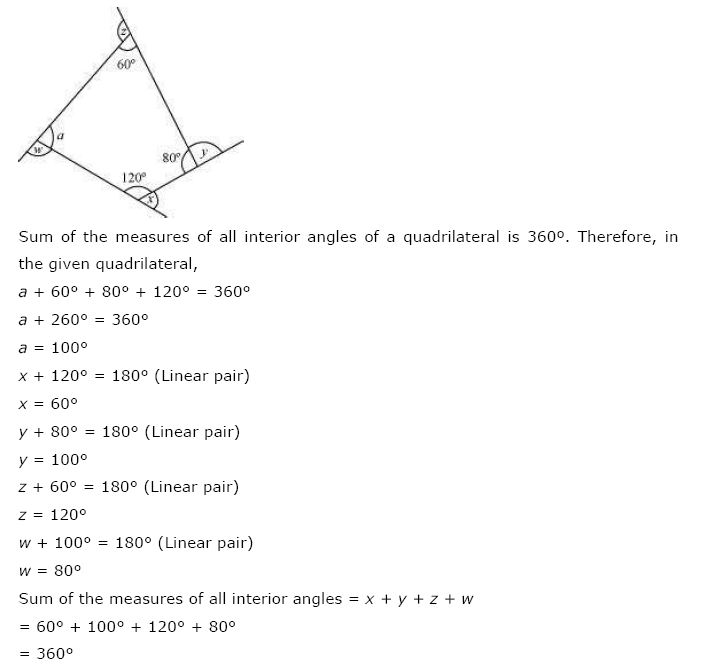
  (b) ∠r + 120° + 80° + 60° = 360° [Angle sum property of a quadrilateral]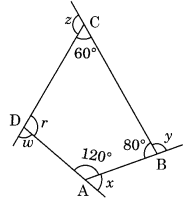
  
  ∠r + 260° = 360°
  ∠r = 360° – 260° = 100°
  Now x + 120° = 180° (Linear pair)
  x = 180° – 120° = 60°
  y + 80° = 180° (Linear pair)
  ⇒ y = 180° – 80° = 100°
  z + 60° = 180° (Linear pair)
  ⇒ z = 180° – 60° = 120°
  w = 180° – ∠r = 180° – 100° = 80° (Linear pair)
  x + y + z + w = 60° + 100° + 120° + 80° = 360°.

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  

  Ch:4 Practical Geometry

• Ex 4.1 Class 8 Maths Question 1.
  Construct the following quadrilaterals.
  (i) Quadrilateral ABCD
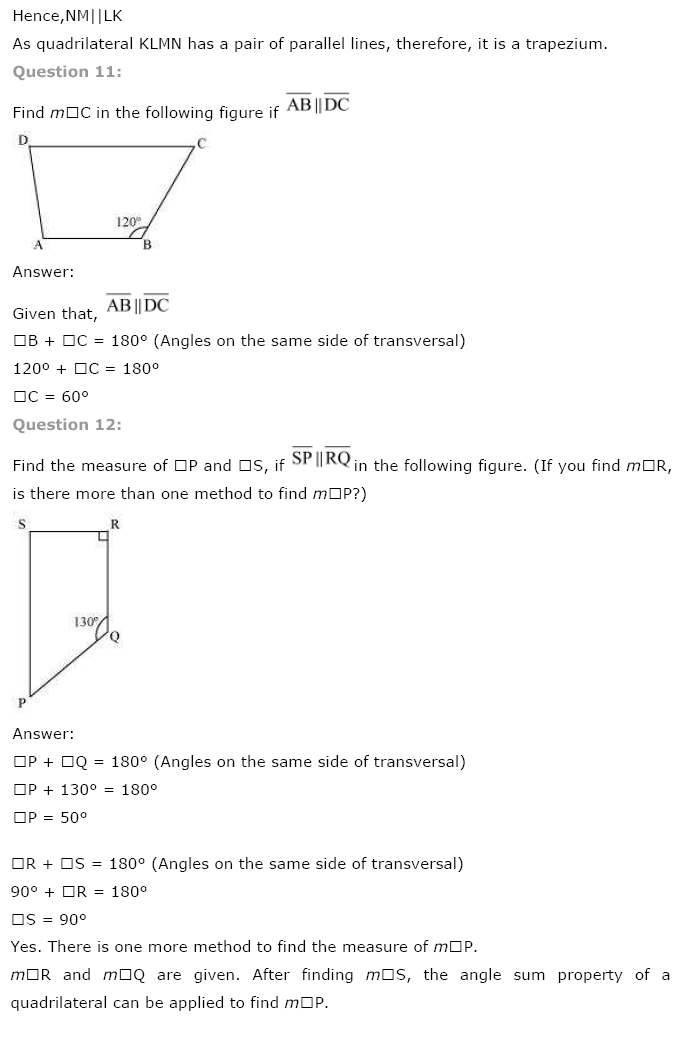
  AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm, AC = 7 cm
  (ii) Quadrilateral JUMP
  JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm, PU = 6.5 cm
  (iii) Parallelogram MORE
  OR = 6 cm, RE = 4.5 cm, EO = 7.5 cm
  (iv) Rhombus BEST
  BE = 4.5 cm, ET = 6 cm
  Solution:
  (i) We have to draw first rough sketch.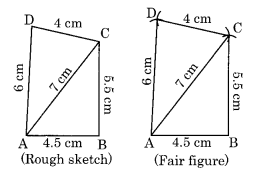
  
  Construction:
  Step I: Draw AB = 4.5 cm
  Step II: Draw an arc with centre B and radius 5.5 cm.
  Step III: Draw another arc with centre A and radius 7 cm to meet the previous arc at C.
  Step IV: Draw an arc with centre C and radius 4 cm.
  Step V: Draw another arc with centre A and radius 6 cm to cut the former arc at D.
  Step VI: Join BC, AC, CD and AD.
  (ii) We have to draw the first rough sketch.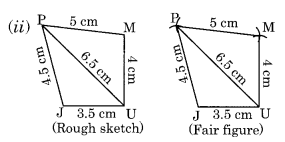
  
  Thus ABCD is the required quadrilateral.
  Construction:
  Step I: Draw JU = 3.5 cm.
  Step II: Draw an arc with centre J and radius 4.5 cm.
  Step III: Draw another arc with centre U and radius 6.5 cm to meet the previous arc at P.
  Step IV: Join JP and UP.
  Step V: Draw an arc with centre U and radius 4 cm.
  Step VI: Draw another arc with centre P and radius 5 cm to meet the previous arc at M.
  Step VII: Join UM and PM.
  Thus, JUMP is the required quadrilateral.
  (iii) We have to draw the first rough sketch.
  
  Construction: (Opposite sides of a parallelogram are equal)
  Step I: Draw OR = 6 cm.
  Step II: Draw an arc with centre R and radius 4.5 cm.
  Step III: Draw another arc with centre O and radius 7.5 cm to meet the previous arc at E.
  Step IV: Join RE and OE.
  Step V: Draw an arc with centre E and radius 6 cm.
  Step VI: Draw another arc with centre O and radius 4.5 cm to meet the former arc at M.
  Step VII: Join EM and OM.
  Thus, MORE is the required parallelogram.
  (iv) We have to draw first rough sketch.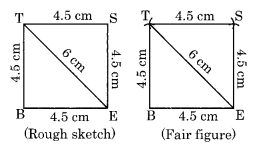
  
  Construction: (All sides of a rhombus are equal)
  Step I: Draw BE = 4.5 cm
  Step II: Draw an arc with centre B and radius 4.5 cm.
  Step III: Draw another arc with centre E and radius 6 cm to meet the previous arc at T.
  Step IV: Join BT and ET.
  Step V: Draw two arcs with centres E and T with equal radii 4-5 cm to meet each other at S. .
  Step VI: Join ES and TS.
  Thus, BEST is the required rhombus.

  
  

  

  

  

•